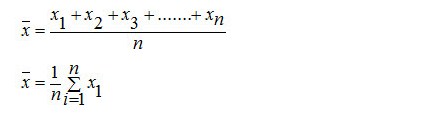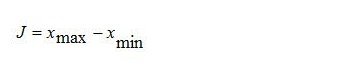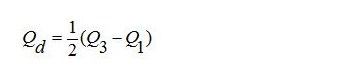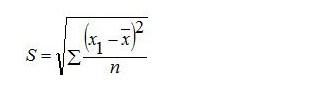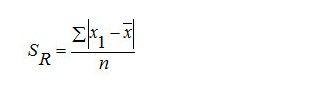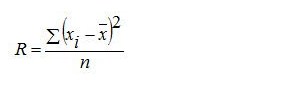Showing posts with label KALKULUS. Show all posts
Showing posts with label KALKULUS. Show all posts

June 13, 2018

Teorema Dasar Kalkulus

No comments
Teorema :
Jika f kontinyu pada [a, b] dan F anti turunan f pada [a, b] maka \int_{a}^{b} f(x) dx = F(b) – F(a)
Bukti :
Akan ditunjukkan \lim_{\left \| p \right \|\to 0} \sum_{k=1}^{n}f(\hat{x_{k}})\bigtriangleup x_{k} = F(b) – F(a)
Diambil P, n-partisi pada [a, b], yaitu :
a = x0 < x1 < x2 < … < xk-1 < xk < … < xn-1 < xn = b
Perhatikan :
F(b) – F(a) = F(xn) – F(x0)
            = \sum_{k=1}^{n} [F(xk) – F(xk-1)]
Mengingat f kontinyu pada [a, b], maka F juga kontinyu pada interval tersebut sebab F antiturunan f. Berarti F kontinyu pada tiap sub interval [xk-1, xk] , k = 1, 2, .., n. Berdasarkan Teorema Nilai Rata-Rata untuk turunan, maka terdapat titik \hat{x_{k}} \quad \epsilon (xk-1 ,xk) sedemikian sehingga.
        F'(\hat{x_{k}}) = \frac{F(x_{k})-F(x_{k-1})}{x_{k}-x_{k-1}}
        \Leftrightarrow F(xk) – F(xk-1) = F'(\hat{x_k})(xk – xk-1)
        \Leftrightarrow F(xk) – F(xk-1) = f(\hat{x_k}) \bigtriangleup xk
Jadi diperoleh :
    F(b)-F(a) = \sum_{k=1}^{n} [F(xk) – F(xk-1)]
              = \sum_{k=1}^{n} f(\hat{x_k}) \bigtriangleup xk
dan bila kedua ruas diambil \left \| P \right \|\rightarrow 0 maka :
    \lim_{\left \| p \right \|\to 0} \sum_{k=1}^{n} [F(b) – F(a)] = \lim_{\left \| p \right \|\to 0} \sum_{k=1}^{n} f(\hat{x_k}) \bigtriangleup xk
    F(b) – F(a) = \lim_{\left \| p \right \|\to 0} \sum_{k=1}^{n} f(\hat{x_k}) \bigtriangleup xk \blacksquare
Dengan Teorema Dasar Kalkulus untuk integral tersebut, maka perhitungan integral untuk fungsi-fungsi kontinyu, tidak lagi serumit perhitungan integral menggunakan Jumlah Rienmann dan semua hasil perhitungan integral tertentu dapat dimanfaatkan.
Fungsi-fungsi yang memenuhi Teorema Dasar Kalkulus tersebut kadang disebut juga fungsi terintegral Newton.
Akibat
Teorema Dasar Kalkulus :
  1. \int_{a}^{a} dx = 0
  2. \int_{b}^{a} f(x) dx = –\int_{a}^{b} f(x) dx
  3. \int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx
Continue reading Teorema Dasar Kalkulus

Teorema Dasar kalkulus

No comments
Teorema Dasar Kalkulus I
Teorema Dasar Kalkulus I menjelaskan bahwa sebuah integral tak tentu dapat dibalikkan dengan menggunakan pendiferensial. Pernyataan Formal dari Teorema Kalkulus I adalah sebagai berikut:
 
“Andaikan f kontinu pada interval tertutup [a,b] dan andaikan x sebarang titik (variable) dalam (a,b). Maka,

Teorema Dasar Kalkulus II
Teorema Dasar Kalkulus berperan sebagai penghubung antara diferensiasi dan integrasi. Bagian teorema ini memiliki aplikasi yang sangat penting, karena ia dengan signifikan mempermudah perhitungan integral tertentu. Pernyataan formal dari Teorema Dasar Kalkulus II adalah :
“Misalkan f kontinu (karenanya terintegrasikan) pada [a,b] dan misalkan F sebarang anti-turunan pada [a,b]. Maka :
Hubungan ini dapat lebih jelas terlihat ketika kita menuliskan kembali kesimpulan untuk teorema dengan f(x)digantikan oleh g(x),

Sekarang, agar lebih paham mengenai teorema dasar kalkulus I dan II, coba perhatikan contoh soal berikut ini :
(Teorema Dasar Kalkulus I )

 
(Teorema Dasar Kalkulus II)


Continue reading Teorema Dasar kalkulus

Rumus Statistika Dasar Matematika Terlengkap

No comments
Rumus Statistika Matematika – Pengertian Statistika ialah ilmu yang mempelajari tentang bagaimana merencanakan, menganalisis, menginterpretasi, mengumpulkan dan mempresentasikan data sehingga bisa dikatakan bahwa Statistika merupakan ilmu yang berkenaan dengan data. Tetapi Statistika dan Statistik merupakan dua hal yang berbeda karena Statistik adalah data, sedangkan Statistika adalah ilmu yg berkenaan dengan data yang dapat digunakan untuk mendeskripsikan atau menyimpulkan data dengan sebagian besar konsep dasarnya mengasumsikan Teori Probabilitas.
Adapun didalam Matematika bahwa Rumus Statistika Dasar ini akan hadir ditingkat Sekolah Menengah Atas (SMA) dan pelajaran Statistika Matematika tersebut meliputi Mean, Median, Modus, Jangkauan, Ragam dan Simpangan sehingga kalian sebagai Siswa dan Siswi tingkat Sekolah Menengah Atas harus benar – benar mengetahui tentang Statistika Matematika Dasar ini atau paling tidak mengenal tentang Mean, Modus dan Median didalam Statistika Dasar.
Hal tersebut dikarenakan Soal – Soal Ujian Akhir Sekolah ataupun Ujian Nasional (UN) Pelajaran Matematika SMA akan ada atau keluar tentang Rumus Matematika Statistika Dasar ini, seperti contohnya menghitung dan mencari Nilai Mean, Modus, Jangkauan, Median ataupun Simpangan. Oleh sebab itu dibawah ini saya sudah memberikan ulasan dan penjelasan tentang Statistika Dasar Matematika seperti Rumus Mencari Mean, Rumus Mencari Modus, Rumus Mencari Median dan lain lain secara lebih lengkap agar kalian dapat memahami tentang Statistika Matematika Dasar.

Rumus Statistika Mencari Mean (Nilai Rataan)

Pengertian dari Mean sendiri adalah nilai rata – rata hitung dan didalam Rumus Mean (Rumus Rataan Hitung) bisa dilakukan dengan cara membagi Jumlah Nilai data dg banyaknya data tersebut. Lalu Rumus Statistika Mencari Rataan Hitung tersebut memiliki tiga rumus yang terbagi antara lain
1. Rumus Rataan Hitung dari Data Tunggal
advertisements
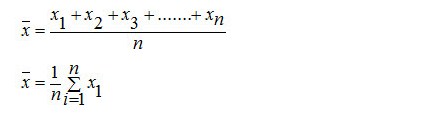
rumus-statistika-mean-data-tunggal
2. Rumus Mean Dari Data Dalam Distribusi Frekuensi

rumus-statistika-matematika-mean-data-distribusi-frekuensi
3. Rumus Mencari Rataan Hitung Gabungan
rumus-mean-rataan-hitung-gabungan

Rumus Statistika Dasar Mencari Modus

Rumus Menghitung dan Mencari Modus terbagi menjadi dua, antara lain pertama Rumus Modus dari Data yang belum dikelompokan yang memiliki artian ukuran yg mempunyai frekuensi tertinggi yang dilambangkan dengan mo.
Rumus Modus yang kedua ialah Rumus Mencari Modus dari Data yg sudah dikelompokkan yang dihitung dengan rumus dibawah ini.
rumus-modus-data-sudah-dikelompokkan

Rumus Statistika Mencari Median

Rumus Mencari Nilai Tengah (Median) dibagi menjadi dua antara lain pertama Rumus Nilai Tengah dari Data yang blm dikelompokkan dengan mencari nilai data yang harus dikelompokan terlebih dahulu dari yg terkecil hingga yg terbesar.
rumus-mencari-median-data-belum-dikelompokkan
Kedua Rumus Median dari data yang telah dikelompokkan.
rumus-median-data-yang-sudah-dikelompokkan
Rumus Jangkauan Statistika Dasar
rumus-jangkauan-statistika-dasar-matematika
Rumus Simpangan Quartil Statistika Matematika
rumus-simpangan-quartil-statistika-dasar
rumus-simpangan-baku-statistika-matematika
Rumus Simpangan Rata – Rata Statistika
rumus-simpangan-rata-rata-statistika-dasar
Rumus Ragam Statistika Matematika
rumus-ragam-statistika-matematika
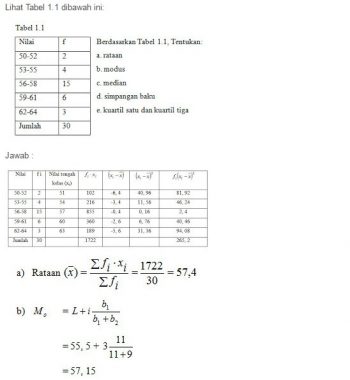
Contoh Soal Statistika Matematika Dasar
contoh-soal-statistika-dasar-matematika rumus-statistika-beserta-contoh-soalnya
Itulah pembahasan yang bisa kami sampaikan dan jelaskan terkait Rumus Statistika Dasar Matematika secara lengkap dan semoga apa yang sudah saya tulis diatas dapat dicerna dan bisa memberikan manfaat untuk kalian para pembaca yang notabenya para pelajar atau Siswa Siswi baik itu tingkat Sekolah Menengah Pertama (SMP) maupun tingkat Sekolah Menengah Atas (SMA) diseluruh dunia karena sudah tugas kami untuk memberikan informasi – informasi yang bermanfaat bagi setiap elegan masyarakat dan kami harapkan Siswa Siswi di Indonesia semua sudah semakin cerdas.
Continue reading Rumus Statistika Dasar Matematika Terlengkap